Bentrand Paradox

Joseph Bentrand
:
1 ê 圓形內底, 畫 1 ê 正 三角形, hit 三 ê 角 hē tī 圓ê 箍線 頂。問題： random 隨機 chhìn-chhài tī chit ê 圓形 線頂 2 點 牽 1 條 直線,  án-ni-siⁿ chit 條 直線 長 ē 比 hit ê三角形 1 條 邊線 khah 長 ê 機率 有 jōa chōe ？

頭 1 ê 解：看 長度,  1：1  -- 1/2

第二 解：看 直線中間點 落 tī toh, 1/4 

第三解： 看 角度, 1/3

Chit 3 種 解答 lóng 真有道理， án-ni, 到底 kám ē-tàng 回答 原本 ê 問題 leh？
ē-sái ê 理由 是 cháiⁿ-iūⁿ？ bōe-sái ê 理由 iū-koh 是 cháiⁿ-iūⁿ ？

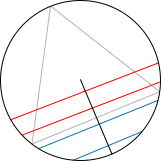
Random chords, selection method 1; red = longer than triangle side, blue = shorter

1. 
   

   Random chords, selection method 2

The "random endpoints" method: Choose two random points on the circumference of the circle and draw the chord joining them. To calculate the probability in question imagine the triangle rotated so its vertex coincides with one of the chord endpoints. Observe that if the other chord endpoint lies on the arc between the endpoints of the triangle side opposite the first point, the chord is longer than a side of the triangle. The length of the arc is one third of the circumference of the circle, therefore the probability that a random chord is longer than a side of the inscribed triangle is 1/3.

The "random radius" method: Choose a radius of the circle, choose a point on the radius and construct the chord through this point and perpendicular to the radius. To calculate the probability in question imagine the triangle rotated so a side isperpendicular to the radius. The chord is longer than a side of the triangle if the chosen point is nearer the center of the circle than the point where the side of the triangle intersects the radius. The side of the triangle bisects the radius, therefore the probability a random chord is longer than a side of the inscribed triangle is 1/2.

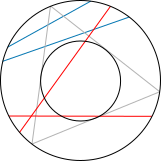
Random chords, selection method 3

The "random midpoint" method: Choose a point anywhere within the circle and construct a chord with the chosen point as its midpoint. The chord is longer than a side of the inscribed triangle if the chosen point falls within a concentric circle of radius 1/2 the radius of the larger circle. The area of the smaller circle is one fourth the area of the larger circle, therefore the probability a random chord is longer than a side of the inscribed triangle is 1/4.